SURVIVING A (TRIG) IDENTITY CRISIS

"If you were stuck on a desert island,
which trig identities would you want to have with you?"

Let's start with some poetry by high school trig students:
one by Elizabeth Palmieri and one by Erin Stanley

Good books, etc. for reference:

  • Most (if not all) precalculus or calculus textbooks have a trigonometry appendix
    (e.g., page A22ff of Stewart, 2nd ed.)
  • CRC Standard Math Tables
    (e.g., 27th edition, page 137ff)
  • A TI-89 or TI-92, which do trig manipulation with tExpand and tCollect
    (below, left)
  • Any other graphing calculator, for verifying trig identities graphically or numerically
    (below, right)
    

Resources on the Web

Web searches for "trig identities" at google.com and at msn.com lead to the following links (and many others):

Building Blocks:
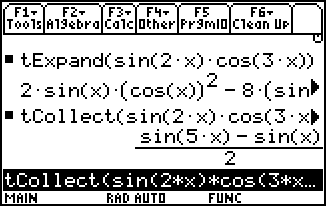
A fundamental set of relationships and identities

  1. SOHCAHTOA (right-triangle trig)
    • ... leads to Pythagorean identities and co-function relationships
    Note: There is no substitute for remembering the basic definitions!
  2. Extending trig functions to the unit circle
    • ... leads to periodicity and reflection relationships [e.g., sin(p–x)=sin x]
  3. Sine and cosine double angle identities (sin 2x = 2 sin x cos x; cos 2x=cos2x – sin2x)
    • ... leads to angle sum/difference formulas, and also to the half-angle formulas for sine and cosine
  4. Others ...?

Application:
CMJ problem 709

Basically, this problem asked for solutions to the equations
(a) p/4 = arctan(q) + arctan(x)

(b) p/4 = arctan(q) + 2arctan(x)
where q and x are both rational ....