![[NB]](../../images/mmca-s.gif) BounceReflections notebook, and are reproduced below.
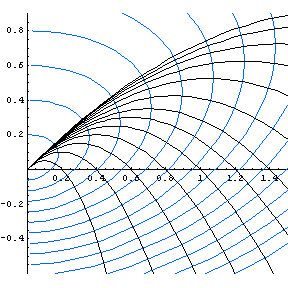
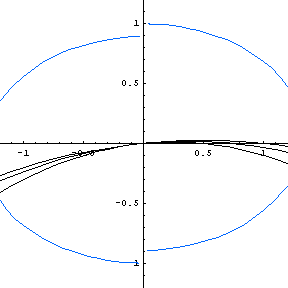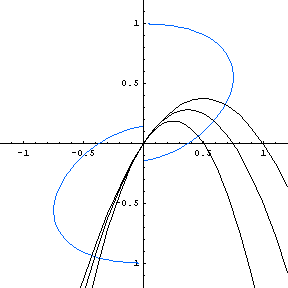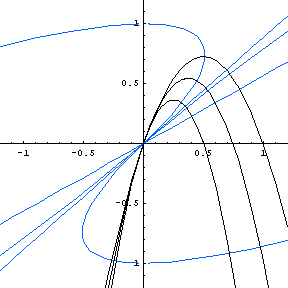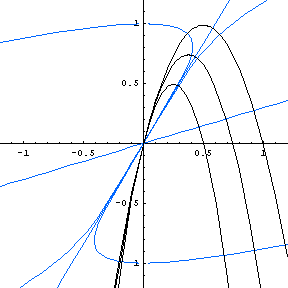
BounceReflections notebook, and are reproduced below. | Shown in blue is a family of "reflecting walls" for the family of curves representing the path of a ball thrown from the origin at a 45-degree angle, with varying initial velocity. Every such parabola crosses these curves at right angles—so if there were a wall of this shape, a perfectly elastic ball would bounce back to the origin ("reflect"). |
 |
Here is an animated GIF file that shows the changing shape of the reflecting wall (or rather, one
member of the family of reflecting walls) as the initial angle varies. Notice the change that occurs
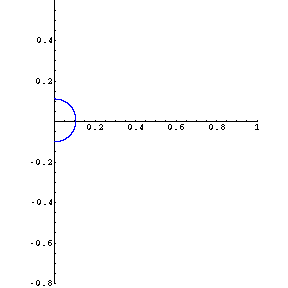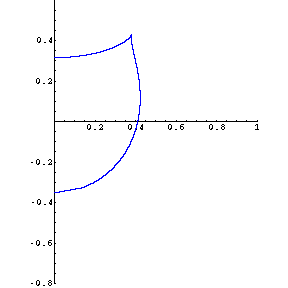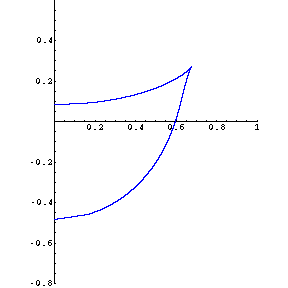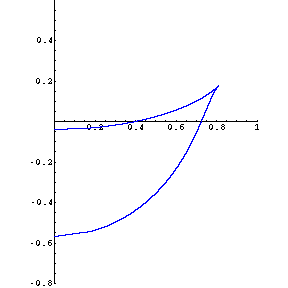
at an angle of about 70.5 degrees (when the initial slope of the throw is 81/2)—suddenly
the character (and number) of reflecting walls changes, as first one line, then two lines are reflecting
walls, and the curve acquires "tails" in quadrants II and IV. (In fact, those tails eventually cross
over into the first and third quadrants, and are asymptotic to the shallower-sloped line.) Formulas
for these curves are derived in the
![[NB]](../../images/mmca-s.gif) BounceReflections notebook, and are reproduced below. BounceReflections notebook, and are reproduced below. |
The parametric representations of the reflecting walls (variable velocity, fixed angle α, with m = tan α) are x = K f(t) and y = tx, where K is a non-zero constant, and
![[FORMULAS FOR f(t)]](reflectingformula.gif)
Additionally, for m2 >= 8, the line(s) y = t*x are reflecting walls, where the slope(s) t* is(are) the excluded value(s) in the definition of f(t). Finally, for the case m2 = 8, we have the alternate parametrization:
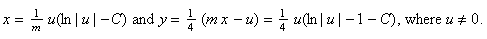
 |
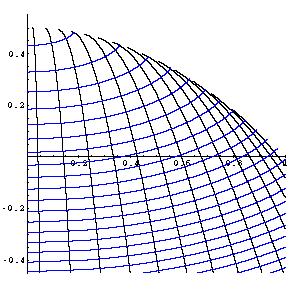 |
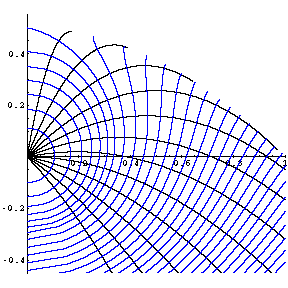
If we vary the angle (but hold velocity fixed), there are two families of reflecting walls. The first family, shown in blue on the far left, is orthogonal to each parabola up until that parabola touches the envelope of the family of parabolas (that is, for x < cot α, where α is the initial angle of the ball, or for all x, if α < 0). The other family of OTs are orthogonal to parabolas after they touch the envelope (for x > cot α, provided α > 0). These two families of OTs correspond to the level curves of the function where v = x2 and u = ±√(1 – 2y – x2). The pre-envelope OTs correspond to u < 0, and the post-envelope OTs correspond to u > 0. |
Balls Bouncing on Slanted Walls
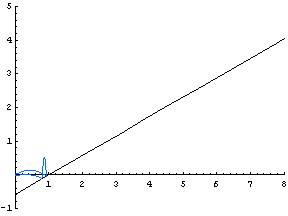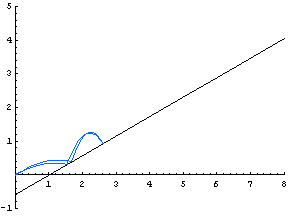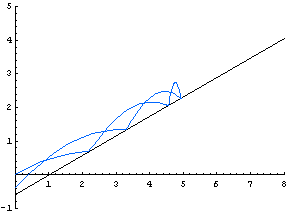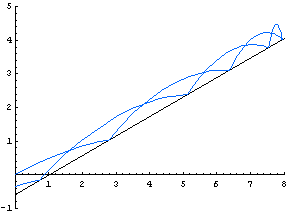 | This animated GIF file shows how the path of a ball varies as the initial velocity changes. (The initial angle of the ball, and the angle of the wall, is π/6.) |
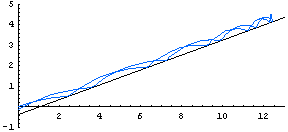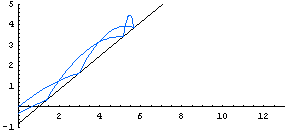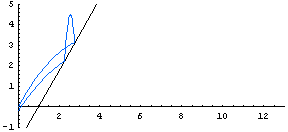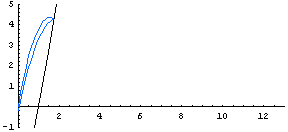 | Here we see how the path of a ball varies when the initial velocity is fixed, but the initial angle of the ball (and the angle of the wall) varies. |